Сингулярные возмущения в математике и физике

C.н.с. Никулин Е. И.

C.н.с. Орлов А. О.

В последние годы, в связи с потребностью таких областей научного знания, как биофизика, химическая кинетика, астрофизика, геология, физика полупроводников и т.д., возрастает интерес к сингулярно возмущенным дифференциальным уравнениям. Теория сингулярных возмущений – одно из тех научных направлений на кафедре математики, которые выросли из пионерских работ А. Н. Тихонова, В. Ф. Бутузова, Н. Н. Нефёдова и А. Б. Васильевой. Суть названия состоит в том, что малое (в определённом смысле) возмущение, добавленное в уравнение, может существенно повлиять на поведение решения. Такие уравнения являются эффективными инструментами математического моделирования, поскольку с их помощью можно описывать физические величины, резко изменяющиеся от одного уровня насыщения до другого, при этом особое внимание уделяя области перехода.

Широкое применение в математическом моделировании находят функции вида контрастных структур. Контрастными структурами называются функции, в области определения которых есть подобласти, в которых эти функции имеют большие градиенты.  Эти подобласти называются внутренними переходными слоями.  Ширина переходного слоя как правило много меньше ширины рассматриваемой области, поэтому в задачах с решениями вида контрастных структур всегда можно выделить малый параметр. Задачи с малым параметром можно исследовать аналитически при помощи асимптотических методов. В частности, метод дифференциальных неравенств позволяет получить условия существования решений вида контрастных структур и устойчивости стационарных контрастных структур. Эти условия необходимо учитывать  при разработке математических моделей, описывающих резкие изменения физических величин на границах раздела сред. Например, температура на границе вода-воздух, для которой была предложена модель на основе уравнения теплопроводности с разрывным коэффициентом диффузии и разрывным источником. На рисунке график распределения температуры в приграничном слое шириной 10 см вблизи раздела вода-воздух в случае, когда температура воды меньше температуры воздуха. Красные точки – экспериментальные замеры, черная сплошная линия – результат численного расчета согласно представленной модели.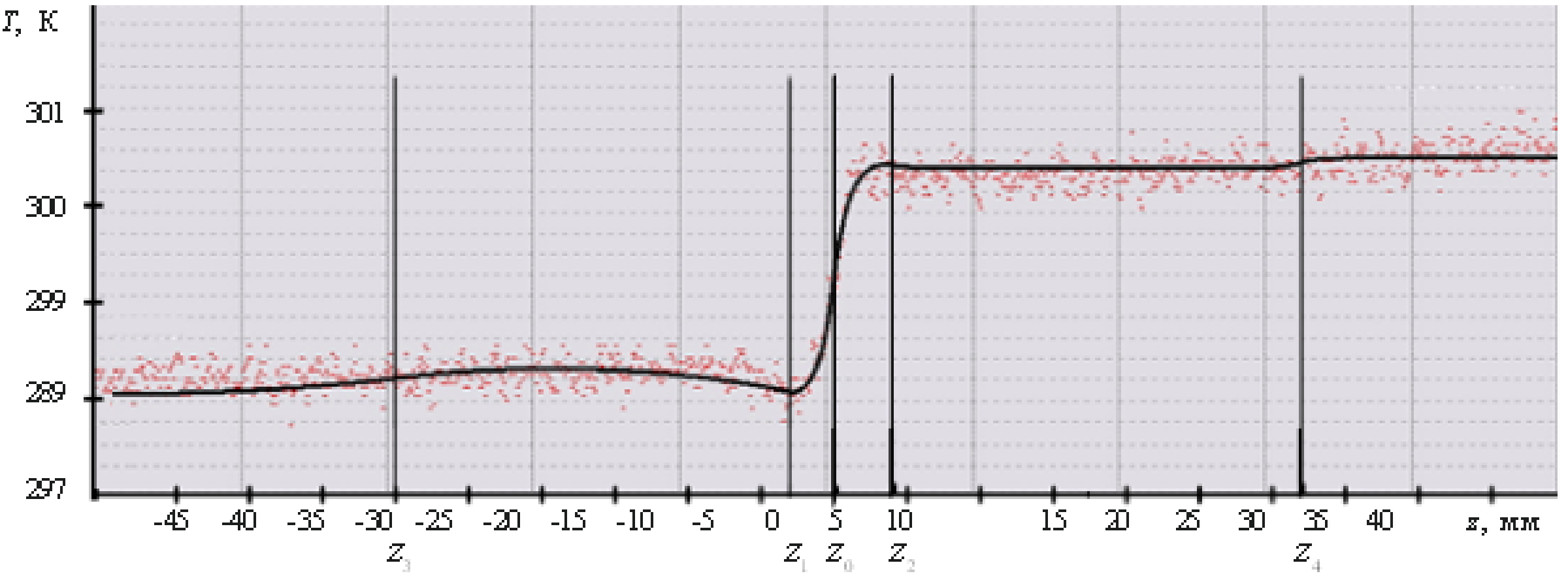

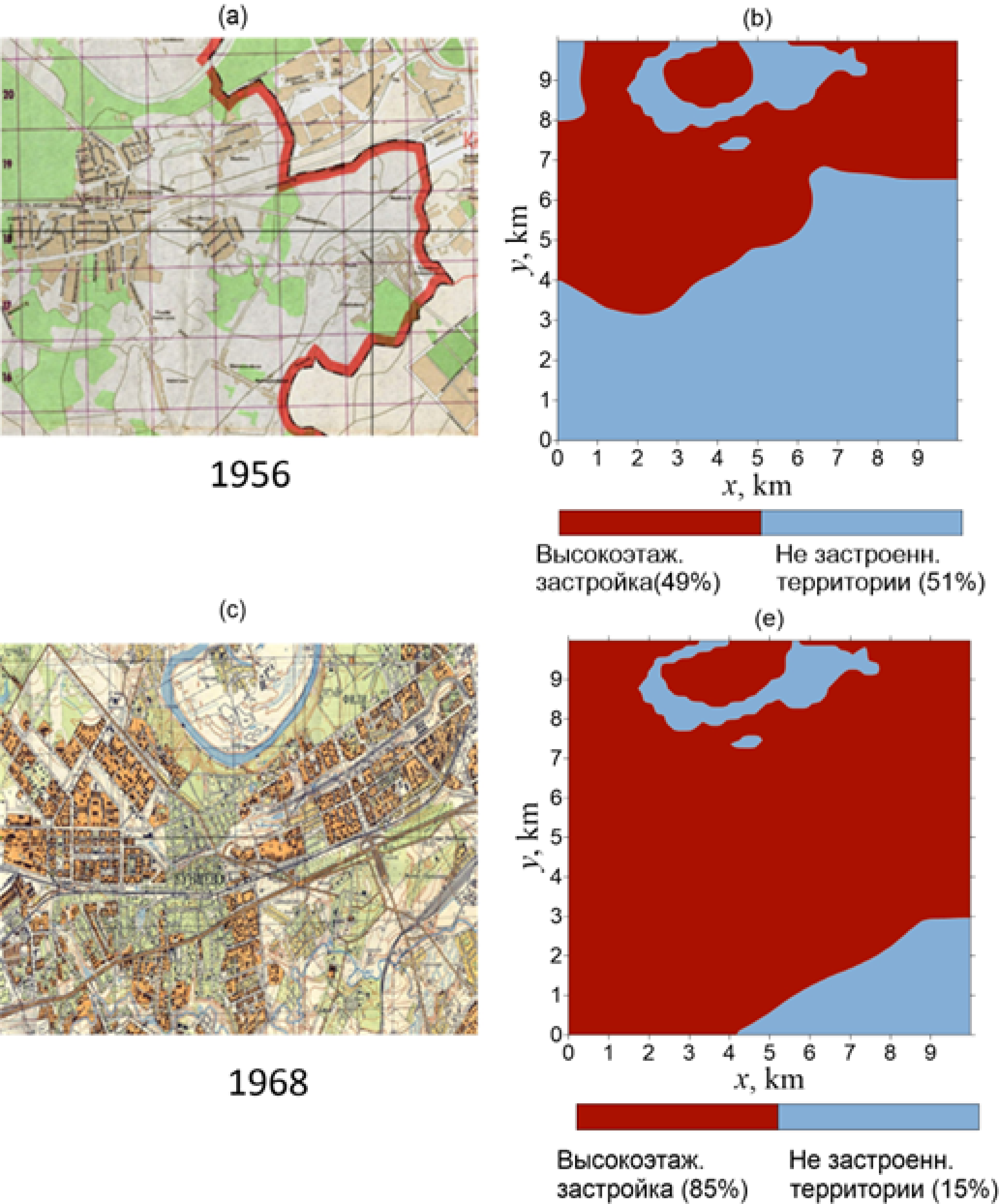Ещё один пример моделирования с использованием теории контрастных структур – модель развития мегаполисов. На рисунке – последовательные этапы присоединения Кунцево к Москве: 1956 год и 1968 год. В левой части – карты района Филе-Кунцево, на рисунках в правой части красным цветом указана область городской застройки согласно модели.

Важное место среди приложений этих уравнений занимают нелинейные модели переноса заряда и тепла в электропроводящих материалах: металлах, полупроводниках, сверхпроводниках, низкоразмерных системах (графен и др.). Асимптотическое исследование таких моделей представляет большую актуальность в связи с широким применением этих материалов в современной электронике, а также большим потенциалом их практического использования в различных отраслях промышленности. Например, в графене наличие областей с большими градиентами температуры приводит к возникновению в них больших плотностей фототока, что особенно важно при проектировании прототипов фотодетекторов для среднего инфракрасного диапазона, использующегося в приборах ночного видения.